Todos conocemos las dificultades que entraña la resta con canje en los primeros grados. Sin quererlo prolongamos una larga tradición de formas de abordar esta operación reducida a pasos que se dan sin entender la lógica detrás. Pensemos en el caso de la sustracción 54 - 19. Al colocar estos valores en columna notamos que en la de las unidades la resta 2 - 9 no resulta posible. El 5 entonces presta 1 al 4 y, por supuesto, trazamos ese 1 más pequeño junto al 4 para que no haya duda que se ha convertido en 14.
Una comprensión más flexible de la forma en que se componen los números resulta imprescindible para entener cómo funciona el algoritmo.
Expresemos la sustracción anterior con los números descompuestos en decenas (D) y unidades (U). La imposibilidad de restar 4 - 9 se supera si es que logramos descomponer de un modo alternativo al número 54, como se muestra a continuación:
Descomposición convencional Descomposición no convencional
5S + 4U - 4D + 14U -
1D + 9U 1D + 9U
??? 3D + 5U
¿Cómo podemos desarrollar esta habilidad en el estudiante de descomponer de forma no convencional?
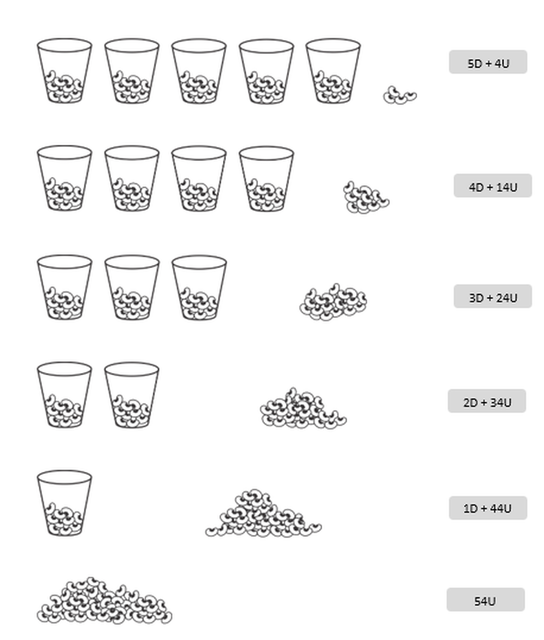
La imagen que acompaña esta entrada es una forma.
Presente cinco vasos con diez frejoles o elementos similares cada uno y fuera de ellos, 4 frejoles sueltos y pida que representen eso en términos de decenas y unidades.
A continuación, vierta el contenido de uno de los vasos junto a los frejoles sueltos iniciales. Pregunte si hay más o menos frejoles que antes. Cuando este claro que hay la misma cantidad, pídales que expresen lo que ven en términos de decenas y unidades. Solicite que continuen la secuencia, virtiendo ellos mismos los vasos que quedan uno a uno y registrando cada paso.